EIGHT GRADE > 8.G.4 > TEACHER GUIDE
TEACHER GUIDE TO CLARIFICATION

8.G.4
Understand congruence and similarity using physical models, transparencies, or geometry software.
8.G.4 Understand that a two-dimensional figure is similar to another if the second can be obtained from the first by a sequence of rotations, reflections, translations, and dilations; given two similar two-dimensional figures, describe a sequence that exhibits the similarity between them.
Verifying Similarity through Properties of Transformations

Similarity
-
Angles congruent, sides are related by scale factor (ratio).
-
A scale factor of 1 will always result in a congruent figure.
-
All regular figures are similar.
Comparing:
Graphs
Tables
Equations
Although this standard appears to be the same as 8.G.2, it differs by two words – similarity and dilation. The focus of 8.G.2 is on congruency as it relates to congruency and a sequence of rigid motions. 8.G.4 deals with similarity as it relates to a sequence of rigid motions and dilations. Scale factor is discussed here and is very closely tied to 7.G.1 which deals with scale drawings and ratios (read more about this connection under the Coherence and Connections section).

To understand this standard it is necessary to understand the definition of similarity and dilation.
Two geometrical objects are called similar if they both have the same shape, or one has the same shape as the mirror image of the other. More precisely, one can be obtained from the other by uniformly scaling (enlarging or shrinking), possibly with additional translation, rotation and reflection. This means that either object can be rescaled, repositioned, and reflected, so as to coincide precisely with the other object.

A dilation is a transformation (notation) that produces an image that is the same shape as the original, but is a different size. A dilation stretches or shrinks the original figure.
8.G.4 This is the students‘ introduction to similarity and similar figures. Students understand similar figures have angles with the same measure and sides that are proportional. Similar figures are produced from dilations. Students describe the sequence that would produce similar figures, including the scale factors. Students understand that a scale factor greater than one will produce an enlargement in the figure, while a scale factor less than one will produce a reduction in size.
Explanations and Examples:
Students build on their experiences with measurement and proportions to notice congruency between shapes and to perform the transformations using measurement tools. In addition, angle types and measurements which is taught in 7th grade is also a pre-requisite for this unit.
Examples:
- Is Figure A similar to Figure A‘? Explain how you know.

-
Describe the sequence of transformations that results in the transformation of Figure A to Figure A’.

Example 1:
Determine if the triangles are similar. Justify your answer.

Explain why this problem is different. Can’t assume right angles. Can’t assume similar without math to back it up

Kansas Association of Teachers of Mathematics (KATM) Flipbooks. Questions or to send feedback: melisa@ksu.edu.
Retrieved from: http://katm.org/wp/wp-content/uploads/flipbooks/8thFlipFinaledited.pdf


If two angles of one triangle are congruent to two angles of another triangle, then the two triangles are similar.
Example 2: Joliet
Rectangle P is dilated about the origin with a scale factor of 0.4 and then reflected over the y-axis. The new image is Rectangle T. Which statements are true about Rectangle P and Rectangle T?
A. They are congruent but not similar because dilation with a scale factor other than 1 changes the lengths of the sides
but not the shape of the figure.
TRUE FALSE
B. They are similar but not congruent because dilation with a scale factor other than 1 changes the lengths of the sides
but not the shape of the figure.
TRUE FALSE
C. They are congruent and similar because the rigid motion did not change the size or shape of the figure.
TRUE FALSE
D. They are neither congruent nor similar because the rigid motion changed the size and the shape of the figure.
TRUE FALSE
Example 3: Taken from PARCC PBA practice problem 14
The figure shows line RS parallel to line UV. The lines are intersected by 2 transversals. All lines are in the same plane.

Part A Explain why triangle RTS is similar to triangle VTU.


Reminder……
A scale factor of one will yield a congruent AND similar figure.
Coherence and Connections: Need to Know
Grade Below
Grade Level
Grade Above
7.G.1
7.G.2
7.G.5
8.G.2
8.G.3
8.G.4
8.G.5
G.CO.2
G.CO.3
G.CO.4
G.CO.5
G.CO.6
G.CO.7
G.CO.8
Students use prior knowledge from sixth and seventh grade related to measurement (congruency) and proportions (dilations). In addition, the work in seventh grade surrounding angle types, i.e. vertical angles, corresponding angles, parallel lines crossed by a transversal, will serve as an anchor to pin the new concepts of congruency and symmetry to.
CCSS.MATH.CONTENT 7.G.1
Solve problems involving scale drawings of geometric figures, including computing actual lengths and areas from a scale drawing and reproducing a scale drawing at a different scale.
In 8th grade students are expected to use what they have learned regarding ratios and proportions as they pertain to scale and scale drawings to assist them in their knowledge of dilation. Students should recognize that a scale factor can either enlarge or shrink a model from work that they have done in 7th grade.
Illinois Assessment of Readiness Evidence Tables: https://www.isbe.net/Documents/IAR-Grade-8-Math-Evidence-State.pdf
Evidence
Statement Key
Evidence Statement Text
Clarifications
MP
8.G.4
Understand that a two-dimensional figure is similar to another if the second can be obtained from the first by a sequence of rotations, reflections, translations, and dilations; given two similar two-dimensional figures, describe a sequence that exhibits the similarity between them.
i) Tasks do not have a context.
ii) Figures may be drawn in the coordinate plane, but do not include the use of coordinates.
iii) Tasks require students to make connections between similarity and transformations.
2,7
Calculator
No
8.C.3.2
Construct, autonomously, chains of reasoning that will justify or refute propositions or conjectures.
Content Scope: Knowledge and skills articulated in
8.G.2, 8.G.4
3,5,6
Yes
8.C.5.2
Apply geometric reasoning in a coordinate setting, and/or use coordinates to draw geometric conclusions.
Content Scope: Knowledge and skills articulated in
8.G.2, 8.G.4
Yes
2,3,5
Classroom Resources
Includes video and games for transformations
Online Math
http://www.onlinemathlearning.com/transformation-similar-8g4.html
HOT Questions
1. This square is divided into five geometric shapes, 4 of which are right triangles.
Are any of the right triangles Similar?
Be prepared to defend your answer.
Answer:
The blue triangle in top right is similar to purple in bottom left. Sides in ration of 2:3

2. Look at the diagram below.
What information must you have to determine if the two triangles are similar? Explain.
Answer:
You either need the measure of two angles or the measure of two sides on each of the triangles.
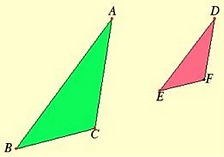
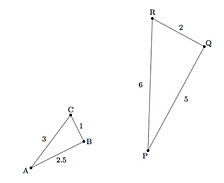
3. Are the triangles similar? If so, what is the scale factor? Explain your reasoning
Answer:
Yes they are similar, scale factor = 2, If I multiply each side of ΔABC by 2, I get the measure of each side in the larger triangle.
4. Dilate rectangle EFGH by a scale factor of 1/2 from the point (0,0).
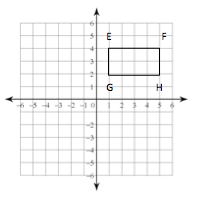
E’_ __(0.5, 2)________
F’ ___(2.5, 2)________
G' ___(0.5, 1)_________
H’____(2.5, 1)_________
a. Record the side lengths of rectangle EFGH here:
b. Record the side lengths of rectangle E’F’G’H’:
c. What did you notice about the side lengths? How does this relate to the dilation?
Answer: They are half as long same as the scale factor.
d. What do we call the relationship between shapes like EFGH and E’F’G’H’?
Answer: Similarity caused by dilation
5. An acute right triangle is rotated 180º around the origin, then it is reflected over the y-axis. Finally it is dilated by a scale factor of 1.5. Circle all of the following that are true.
A. The final image is in the same position as the original image.
B. The final image is larger than the original image.
C. The final image is smaller than the original image.
D. The angles of both the original and final image are congruent.
E. The sides of both the original and final image are congruent.
F. The angles of the final image are 1.5 larger than the original angles
6. Taken from PARCC PBA sample: #15 part b
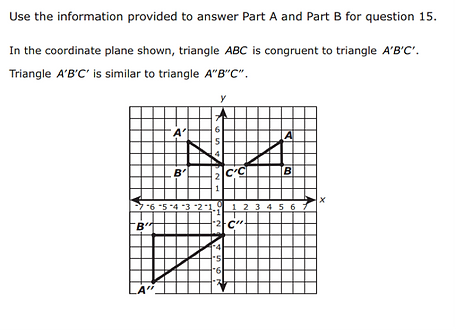
7. Part A is not included because it is about congruency rather than similarity.
Part B
Describe a sequence of transformations that shows that triangle A"B"C" is similar to A'B'C'. Include all the necessary
information to complete each transformation.
Answer:
A’B’C’ was reflected over the x-axis then it was dilated by a scale factor of 2 to create A’’B”C”
Additional Resources
Illustrative Mathematics
http://tasks.illustrativemathematics.org/content-standards/8/G/A/4/tasks/1857
http://tasks.illustrativemathematics.org/content-standards/8/G/A/4/tasks/1946
http://tasks.illustrativemathematics.org/content-standards/8/G/A/4/tasks/1962
Inside Mathematics - Performance Task
https://www.insidemathematics.org/sites/default/files/materials/aaron%27s%20designs_1.pdf
Card Sort (Mars Task) These resources are for use in the classroom with students. The entire lesson is explained and scripted on the site.
http://map.mathshell.org/materials/download.php?fileid=1372
Also check out Student Achievement Partners Coherence Map.
