FIFTH GRADE > 5.NF.5a > TEACHER GUIDE
TEACHER GUIDE TO CLARIFICATION

5.NF.5a
Apply and extend previous understandings of multiplication and division to multiply and divide fractions.
5.NF.5a Interpret multiplication as scaling (resizing) by:
-
Comparing the size of a product to the size of one factor on the basis of the size of the other factor, without performing the indicated multiplication.
Without Performing the Indicated Multiplication
Connect the meaning of multiplication and division of fractions with whole-number multiplication and division. Consider area models of multiplication and both sharing and measuring models for division.
Remember students may believe that multiplication always results in a larger number. Using models when multiplying with fractions will enable students to see that the results will be smaller. Additionally, students may believe that division always results in a smaller number. Using models when dividing with fractions will enable students to see that the results will be larger.
Example:
How does the product of 225 x 60 compare to the product of 225 x 30? How do you know? Since 30 is half of 60, the product of 225 x 60 will be double or twice as large as the product of 225 x 30.
× 7 is less than 7 because 7 is multiplied by a factor less than 1 so the product must be less than 7.
7

of 7
Example:
-
Mrs. Bennett is planting two flowerbeds. The first flowerbed is 5 meters long and 6/5 meters wide. The second flowerbed is 5 meters long and 5/6 meters wide. Which area is larger than 5 square meters? The 5 meters long and 6/5 meters wide area is larger than 5 square meters because you are multiplying by a value larger than one.
-
Is 2 x 8 more or less than 8? 2 x 8 must be more than 8 because 2 groups of 8 is 16 and 2 is almost 3 groups of 8. So the answer must be close to, but less than 24.
-
Is X more or less than ?
= because multiplying by is the same as multiplying by 1.
Kansas Association of Teachers of Mathematics (KATM) Flipbooks.
Questions or to send feedback: melisa@ksu.edu. Retrieved from Math Flipbooks.
This Standard connects to Mathematical Practice Standard 7 because students need to see the pattern of multiplication. They need to recognize that when you multiply by a form of one, the value of the number will not change due to the identity property. When multiplying X by a number less than one the product will be less than X and when multiplying X by a number greater than one the product will be greater than X. If students do not recognize this structure, they will not be able to answer questions without performing the multiplication.
For additional information go to Achieve the Core.
Coherence and Connections: Need to Know
Grade Below
Grade Level
Grade Above
3.OA.1
3.OA.2
4.OA.1
4.OA.2
4.NF.1
4.MD.2
5.NF.5a
5.NF.3
5.NF.4
5.NF.6
5.OA.2
6.RP.1
Evidence
Statement Key
Evidence Statement Text
Clarifications
MP
5.C.7.1
Distinguish correct explanation /reasoning from that which is flawed, and – if there is a flaw in the argument – present corrected reasoning. (For example, some flawed ‘student’ reasoning is presented and the task is to correct and improve it.)
Content Scope: Knowledge and skills articulated in 5.NF.5b
None
3,7,8,6
5.NF.5a
Interpret multiplication as scaling (resizing), by a. Comparing the size of a product to the size of one factor on the basis of the size of the other factor, without performing the indicated multiplication.
i)In so far as possible, tasks are designed to be completed without performing the indicated multiplication
ii) Products involve at least one factor that is a fraction or mixed number.
7,8
Illinois Assessment of Readiness Mathematics Evidence Tables.
Retrieved from: https://www.isbe.net/Documents/IAR-Grade-5-Math-Evidence-State.pdf
Examples of Opportunities for Connections Among Standards, Clusters, or Domains
-
The work that students do in multiplying fractions extends their understanding of the operation of multiplication. For example, to multiply a/b x q (where q is a whole number of a fraction), students can interpret a/b x q as meaning a part of a partition of q into b equal parts (5.NF.4a). This interpretation of the product leads to a product that is less than, equal to or greater than q depending on whether a/b<1, a/b=1 or a/b>1, respectively (5.NF.5).
PARCC Model Content Frameworks: Mathematics Grades 3-11 (version 5). (2017, November).
Retrieved from https://files.eric.ed.gov/fulltext/ED582070.pdf
Also check out Student Achievement Partners Coherence Map.
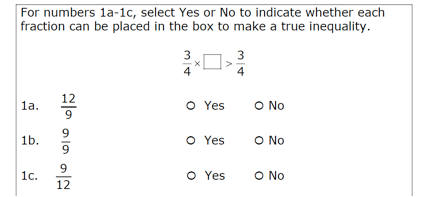


Each day from Monday through Friday, the bakers at Baker’s Square use 1 large sacks of flour to make pie crusts for their awesome pies! Will the bakers use more or less than 5 sacks of flour from Monday through Friday? Explain your answer WITHOUT solving the problem.
Shiloh wants to make 5 pitchers of tea. Each recipe calls for cup of sugar. If she makes 5 pitchers of tea will she have more or less than 1 whole cup of sugar? Explain your reasoning.
-
Prove your answer to “a” by calculating the total number of sacks of flour the bakers will use from Monday through Friday. Show your work.
HOT Questions
-
Which of the following expressions would have a greater product? Explain how you know.
x 18
x 18
2. Which expressions are equal to N? In words, explain how you decided.
Additional Resources
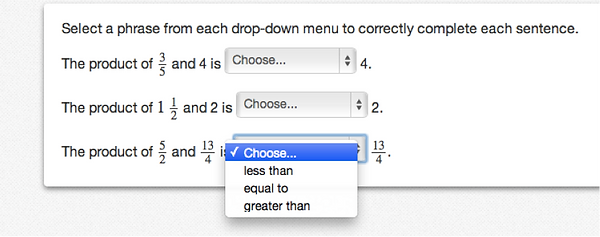
Illustrative Mathematics
http://tasks.illustrativemathematics.org/content-standards/5/NF/B/5/tasks/22
http://tasks.illustrativemathematics.org/content-standards/5/NF/B/5/tasks/49
http://tasks.illustrativemathematics.org/content-standards/5/NF/B/5/tasks/143
http://tasks.illustrativemathematics.org/content-standards/5/NF/B/5/tasks/150
http://tasks.illustrativemathematics.org/content-standards/5/NF/B/5/tasks/151
http://tasks.illustrativemathematics.org/content-standards/5/NF/B/5/tasks/164
http://tasks.illustrativemathematics.org/content-standards/5/NF/B/5/tasks/1174
http://tasks.illustrativemathematics.org/content-standards/5/NF/B/5/tasks/2101
Howard County

